Introduction

What a recommender system tries to do is suggest to users items that can be relevant for the specific user. There are two main approaches to account for this task, content-based approach that uses features to infer user-item interaction (for example, to recommend teenager movies to young people having the age information), and the collaborative filtering approach, which instead stores the past interactions between users and items in a matrix, and using the latter, produces new recommendations. In a recommender system, items can be anything, from movies to music; an interesting task is when items are hotel clusters as in Expedia Hotel Recommendations Kaggle challenge where the goal is to predict in which of the provided 100 hotel clusters a user might book a hotel.

To deepen recommender systems, not only did I decide to develop a collaborative filtering model for my project, but I also content-based models to solve the task. The implemented models consist in:

Alternating Least Square for the collaborative filtering approach, and
both Logistic regression and Random Forest for the content-based approach.

Data Analysis

The provided training dataset is composed of two files:

train.csv, which includes the searches of the users and the features about how a user interacts with the results, and
destinations.csv, where for each destination there are latent features extracted from the reviews about the hotel services.

The former is composed of twenty-four features that represent stay, geographical and temporal information like for example:

the number of rooms and people as stay information
the check-in and check-out dates and the timestamp as temporal information
id of the hotel continent or the country as geographical information In the dataset, also information about how the user interacts with the result is included, like if from a search the user books the hotel or not.

Feature name	Description
date_time	Timestamp
site_name	ID of the Expedia point of sale (i.e., Expedia.com, Expedia.co.uk, Expedia.co.jp, …)
posa_continent	ID of continent associated with site_name
user_location_country	The ID of the country the customer is located
user_location_region	The ID of the region the customer is located
user_location_city	The ID of the city the customer is located
orig_destination_distance	Physical distance between a hotel and a customer at the time of the search. A null means the distance could not be calculated
user_id	ID of user
is_mobile	1 when a user connected from a mobile device, 0 otherwise
is_package	1 if the click/booking was generated as a part of a package (i.e., combined with a flight), 0 otherwise
channel	ID of a marketing channel
srch_ci	Check-in date
srch_co	Check-out date
srch_adults_cnt	The number of adults specified in the hotel room
srch_children_cnt	The number of (extra occupancy) children specified in the hotel room
srch_rm_cnt	The number of hotel rooms specified in the search
srch_destination_id	ID of the destination where the hotel search was performed
srch_destination_type_id	Type of destination
hotel_continent	Hotel continent
hotel_country	Hotel country
hotel_market	Hotel market
is_booking	1 if a booking, 0 if a click
cnt	Number of similar events in the context of the same user session
hotel_cluster	ID of a hotel cluster

Since some features are not ready to be fed to a model, like dates, some features extraction is needed.

Features extraction

First of all, after some attempts, I found out that there were some spurious entries in which the check-out date came before the check-in date, so due to the irrelevant number of them with respect to the huge amount of positive entries, I removed these from the training dataset.

After that, from the remaining ones, I extracted some additional features:

the length of the stay in day computed as the difference between the check-out and the check-in dates
the month of the stay given by the month of the check-in date
the year of the stay computed as the year of the check-in date
the number of remaining days between the search and check-in date

Additionally, since in the dataset for a user there could be multiple searches for the same destination with the same period and the same number of people, I opted to group these instances to obtain only an aggregated entry; Doing this, I have to create new features to avoid loss of information. In this regard, the following new features are computed:

the number of bookings that the user made for that destination computed as the sum of the feature is_booking
the number of clicks that the user made for that search computed as the occurrences of the feature is_booking
the relevance of the destination is computed as the number of bookings plus the number of clicks times 0.1. Namely, every ten clicks are considered a book

Features imputation

Since initially there were some missing values in the check-in and check-out dates in some of the aggregated entries, there could be missing values. In particular, in the srch_days, srch_month, srch_year and days_before_leaving when a missing value appears, I fill it with the mode value for the respective destination of the search.

Moreover, not all destinations have the corresponding latent features. Even in this case, when there is no value, I replace them with the mean of the respective hotel continent and country of the search because intuitively, these two features should be significant ones for the destination.

Dimensionality reduction

After that, considering a large number of latent features for each destination, and the fact that they must be joined with the trained dataset features, to avoid having a significant number of features, a linear dimensionality reduction technique named Principal Component Analysis is applied in order to represent the latent features in a low dimensional space. In addition, using this technique, the use of unnecessary information is prevented, and also the variance between data is preserved.

Almost ready for training

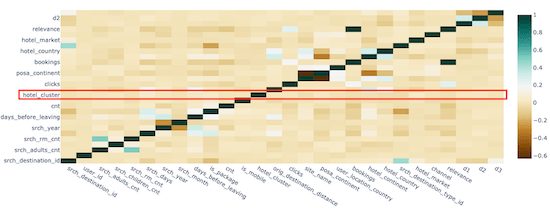
Before starting with the training phase, the correlation matrix that underlines the negative and positive correlations between each feature is inspected, and except for some expected correlations (like the number of the rooms is positively correlated with the number of adults and children, meaning that, the number of rooms depends on how many adults and children there are), there are no relevant correlations between hotel_cluster and the other features. This means that the task is not easy to account for since the relationships between hotel clusters and the other features are not so evident.

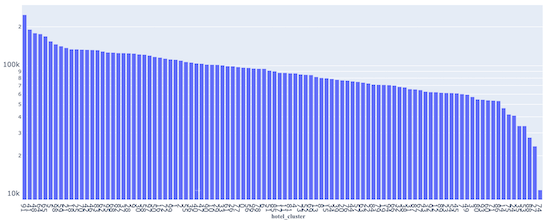
The last check to do is about the distribution of the labels, and as can be seen in the following log-scale plot, data are well distributed over the one hundred classes. Another important thing highlighted from the following plot is that the majority class is represented by the cluster with id 91, while the minority class is the cluster with id 74.

Models

An Alternating Least Square model is used to investigate the collaborative filtering approach, but since it is used to give ratings (regression algorithm), it is also incompatible with the classification nature of the task. So, what I have done is consider the task anyway as a regression one using implicit feedback, but the drawback is that there is no ground truth and so no way to quantitatively evaluate the performances of the model.

Furthermore, considering the task as a multi-class classification one, two different models can be used to study the content-based approach, namely Logistic Regression and Random Forest models.

Alternating Least Square

In a collaborative filtering setting, given the user-item matrix that contains the interactions between them, we have that the ratings which a user gives to items can be explicitly or implicitly provided by the dataset. In the latter, the ratings are inferred from some actions, for example, the number of clicks on an item. The aim of this approach is to predict ratings, and a common way to do it is using Matrix Factorization. The idea of this technique is to find two lower dimensional matrices, $\mathbf{U}$ and $\mathbf{I}$, to represent the original user-item matrix $\mathbf{R} \in \mathcal{R}^{n \times m}$, where

$\begin{align*} \mathbf{U} &\in \mathcal{R}^{n \times k} \end{align*}$ , each line represents a user
$\begin{align*} \mathbf{I} &\in \mathcal{R}^{k \times m} \end{align*}$ , each column represents an item

$k$ represents the number of latent features which should retain the dependencies and the properties of $\mathbf{R}$.

In this way, to predict a rating that a user $\mathbf{u}_p$ gives to an item $\mathbf{i}_q$ is obtained by the inner product between the two vectors

\[\begin{equation*} \hat{r}_{pq} = \mathbf{u}_p^{\top} \cdot \mathbf{i}_q = \sum_{k} u_{p,k} i_{k, q} \end{equation*}\]

So, given that we want to estimate the complete user-item matrix $\mathbf{R}$ we can formulate this problem as an optimization one, trying to minimize the \emph{Least Square Error} of the predicted ratings

\[\begin{equation*} \min_{\mathbf{u}, \mathbf{i}}\sum_{p=1}^n\sum_{q=1}^m\left( r_{p,q} - \mathbf{u}_p^{\top} \cdot \mathbf{i}_q \right)^2 \end{equation*}\]

Note that the gradient descent is only an approximate approach given the non-convexity of the objective function; but if we consider as constant one of the two involved vectors, namely $\mathbf{u}$ or $\mathbf{i}$, and update the other one, the objective function is convex. Therefore, Alternating Least Square is a two-step iterative optimization algorithm, working as follow:

fix a latent vector, for example, $\mathbf{u}$ and optimize for the other vector $\mathbf{i}$;
then, vice versa, fix the latent vector $\mathbf{i}$ and optimize for $\mathbf{u}$

These steps are repeated until convergence.

Logistic Regression

About the content-based approach, we consider the task as a multi-class problem with 100 different classes, namely one per hotel cluster. The generalization of the Logistic Regression in multi-class problems is the Multinomial Logistic Regression, where:

first, the scores, using linear predictor function, are computed

\[\begin{equation*} f(k, i) = \pmb{\beta}_k \cdot \mathbf{x}_i \text{ ,} \end{equation*}\]

where $\pmb{\beta}_k$ is the matrix of the weights associated with outcome k;

then, to get the conditional probabilities, the softmax function is applied

\[\begin{equation*} P(\mathbf{Y}=k | \mathbf{X}=\mathbf{x}_i, \pmb{\beta}) = \psi(f(k, i)) = \frac{e^{\pmb{\beta}_k \cdot \mathbf{x}_i}}{\sum_{k'=1}^K e^{\pmb{\beta}_{k'} \cdot \mathbf{x}_i}} \end{equation*}\]

The predicted class is the one with the highest probability.

Random Forest

Also, the Random Forest model is considered because most of the features are categorical, and since it is a tree-based model, it could perform well in such a scenario. Random Forest is an ensemble of Decision trees where each of them is uncorrelated from the others. Each decision tree that composes the forest makes predictions using a random subset of the initial features, and the decision of splitting a node is given by considering the Gini index that ranges in zero-one and expresses the purity of classification, namely when Gini index is zero means that all the elements belong to a certain class when it is one means that elements randomly belong to different classes and when it is one half means an equal distribution of the elements in some classes.

\[\begin{equation*} I_G(\mathcal{D}_{R_j}) = \sum_{k=1}^K \hat{p}_{jk} \left( 1 - \hat{p}_{jk} \right) \end{equation*}\]

The overall outcome is given by the majority voting of the predictions of the decision trees.

Results

As previously said, there is no way to evaluate the performance of the ALS model with a metric, given the lack of ground truths since what the model recommends are destinations id, but the ground truths are hotel clusters. Thus, to have an idea of how the model performs, I selected a subset of users with the corresponding mode of hotel continent and country, so I took users with the ids of the continent and the country in which they searched the most. Then I recommended five destination ids, and for each, I also took its continent and country to see if the model recommends in a reasonable way.

user_id	recommendations, hotel_continent, hotel_country
420704	[[8791, 4, 8], [8267, 2, 50], [11439, 4, 163], [11938, 4, 8], [5405, 4, 8]]
197505	[[8745, 6, 204], [8253, 6, 70], [8788, 6, 77], [8268, 2, 50], [8746, 6, 105]]
365251	[[8267, 2, 50], [8253, 6, 70], [8745, 6, 204], [7635, 2, 50], [8788, 6, 77]]

What we can see is, for example, in the first line, most of the suggested destinations are in the continent in which the user has done most of the searches.

These experiments are not so meaningful, but they can give an idea of how the model performs.

Regarding the Logistic Regression model, it was trained for a maximum of one hundred epochs taking about one hour and a half, yielding the following results

Accuracy	0.245
F1	0.208
PrecisionByLabel	0.238

which, as can be seen, are not good results as expected.

Finally, the Random Forest model is composed of 70 decision trees where each of these has a maximum depth equal to 10, taking quite a long time to train but yielding more significant results outperforming the other two approaches

Accuracy	0.687
F1	0.633
PrecisionByLabel	0.785

From the following model, I also extracted the five most relevant features:

hotel_market
hotel_continent
d1
hotel_country
d3

where d1 and d3 are the latent features projected onto the first and third components of the PCA.

Conclusions

From the previous results, it can be stated that the Random Forest model outperforms the Logistic Regression one as expected since already from the correlation matrix, hotel_cluster has no linear correlation with any other features and thus modeling the linear relationship between feature is not the right way; while since most of the features are categorical better handling is done by the Random Forest. Another significant result is that by extracting the most important features, we can find that they are all geographical ones. Finally, considering the computed relevant features and the previous results can be said that the Alternating Least Squared model might perform better, but no more significant things can be stated since the evaluation was done on a very restricted test set (only three users) and in particular, no ground truth is provided.

Additional work can be done to improve the results, that is:

over-sample the minority class
even considering other features in the ALS model and not only the destination id and the user-id
try some hybrid model merging collaborative filtering approach and content-based one or also considering some deep learning approach to get better outcomes