Introduction

Image synthesis is a core task in machine learning, and until now, Generative Adversarial Networks have been the state-of-the-art for it; but recently, J. Ho et al. 2020 shows that similar performance can be obtained with a different model, which instead leverages probabilistic diffusion, named in fact Denoising Diffusion Probabilistic Model.

One major application of generative models is dataset augmentation, but in order to generate new images belonging to a certain class, one would need to have a conditional model. The goal of this project is to integrate class-conditionality in probabilistic diffusion models.

Method

A diffusion probabilistic model is a parameterized Markov chain.

The training phase consists of two phases:

a forward pass, also called the diffusion process, Gaussian noise is added to the image according to a fixed schedule so each transition in the Markov chain \(\begin{align*} q(\mathbf{x}_{t}| \mathbf{x}_{t-1}) \end{align*}\) represents the addition of Gaussian noise, and
a reverse pass, where the transitions of a reverse Markov chain are learned in order to reconstruct the destroyed signal

The parameters are learned by optimizing the variational bound on negative log-likelihood:

\[\begin{align*} \mathbb{E}\left[ - \log p_{\theta}(\mathbf{x}_0) \right] &\leq \mathbb{E}_q \left[ - \log \frac{p_\theta (\mathbf{x}_0, \dots, \mathbf{x}_T)}{q(\mathbf{x}_1, \dots, \mathbf{x}_T|\mathbf{x}_0)}\right] \\ &= \mathbb{E}_q\left[ - \log \ p(\mathbf{x}_T) - \sum_{t \geq 1} \log \frac{p_\theta (\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t | \mathbf{x}_{t-1})} \right] \end{align*}\]

Since the parameters for the forward pass are fixed, the only parameters to be learned are the ones of the denoiser, which is based on the popular U-net architecture (O. Ronneberger et al. 2015).

U-Net

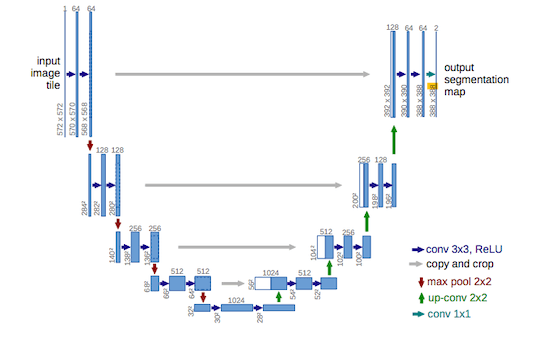
The implementation is based on the GitHub repository denoising-diffusion-pytorch, which provides a working PyTorch baseline.

Conditional Batch Norm

Conditional Batch Norm builds upon Batch Normalization, in which each batch is normalized as follows to reduce the internal co-variate shift:

\[\begin{equation*} \text{BN}_{\gamma, \beta}(x_i) = \gamma_i \frac{x_i - \mathbb{E}(x_i)}{\sqrt{var(x_i)}} + \beta_i \end{equation*}\]

In Conditional Batch Norm, we want to predict \(\gamma\) and \(\beta\) from an embedding of the class so that the class may manipulate entire feature maps by scaling them up or down, negating them, or shutting them off completely.

The integration of Conditional Batch Norm in the architecture is done by replacing the Batch Normalization layers inside the denoiser architecture with conditional ones.

Auxiliary classifier

Following the idea of A. Odena et al. 2016, an extra classifier is added to the denoiser architecture.

With the aim of providing the class information to the latter, the label is embedded, properly reshaped, and concatenated to the channel dimension of the image.

The overall loss is then obtained as a weighted sum of the reconstruction loss and the classifier loss, where the weight is a hyper-parameter. The loss should this way be enriched with class information that should backpropagate to the parameters that are involved in the generation.

Dataset

Our original goal at the start of the project was to apply the model to the insect-pest dataset to create new artificial samples for classification. Nevertheless, the dataset was not large enough to train different unconditional models for each of the classes, and so we instead decided to integrate class conditionality into the model itself. But most of the classes of the dataset had few samples and low variance between them, and it is often hard even for humans to understand what’s in the image.

Therefore, to have a simple benchmark to test our proposed conditional methods, we created an ad-hoc dataset of only two classes with a maximum difference, namely a subset of the Stanford dogs and a subset of the Stanford cars datasets

Results

The unconditional model yielded the following results on the insect-pest dataset

Unconditional results 128 — (Right) ‘Resolution 64 vs (Left) Resolution 128

We can see that by feeding the model with higher resolution images, the results are way more realistic, as the model is able to exploit the larger amount of information given.

Regarding the conditional model, the two proposed methods yielded totally different results.

The next are the results of the Conditional Batch Norm model

CBN dogs results — (Right) ‘Dog’ class vs (Left) ‘Car’ class

CBN cars results — (Right) ‘Dog’ class vs (Left) ‘Car’ class

Despite the fact that the results are somehow funny, we can easily agree with the class generated by the model.

As the reconstruction error is small, the problem seems to be related to the sampling procedure, and indeed it might be the case that the class information is not accounted for correctly during sampling.

To check whether there is a class-related distinction between the generated images, the images are plotted as t-SNE

CBN t-SNE plot

The points seem to be fairly separable, indicating that the class is indeed infused in the generated images.

Instead, the Auxiliary Classifier model results in the converse, yielding more realistic images that do not seem to be much influenced by the class, as we can see from these results

AC dogs results — (Right) ‘Dog’ class vs (Left) ‘Car’ class

AC cars results — (Right) ‘Dog’ class vs (Left) ‘Car’ class

To avoid co-adaptation between the classifier and the generator during training, we pre-trained the classifier on the dataset of real images and then kept its parameters fixed during the training of the rest of the model.

Also, higher-resolution images are fed to the model but with no significant improvement. The generated images, in fact, do not resemble their class, but the classification loss is still able to become really low

AC high res results

Visually inspecting the images turns out that artifacts were present in every image, probably resulting from the generator tricking the classifier, emphasizing features that resulted in high confidence guesses in the latter.

As before, t-SNE is employed to check whether there is a class-related distinction between the images

AC t-SNE plot

As can be seen, this time, the points are all mixed up, indicating that the model fails in conditioning the generation on the class.

Conclusions

The proposed methods do not yield acceptable results, indicating that it is not enough to adapt GANs techniques for class-conditionality to probabilistic diffusion models, while this is also not straightforward to do. This also emphasizes that, while seemingly close to GANs, this family of models requires ad-hoc research, as they are based on different theoretical aspects.